Somewhere on a sphere - math puzzle
What is the mean distance between two randomly choosen points within a sphere of radius 1?
Explanation
This problem is most easily solved by introducing spherical coordinates.
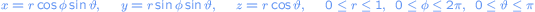
The probability that a randomly choosen point lies in the area of the sphere with sizes
is given by
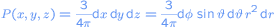
The distance between two randomly choosen points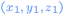
and
within the sphere is
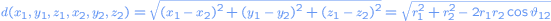
where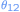
is the angle between the points
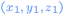and
.
The mean distance between two randomly choosen points within the
sphere is now given by
.
Using spherical coordinates and symmetry, the last formula can be simplified to
.
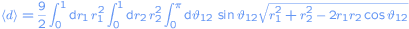Performing the integral over the angle gives
.
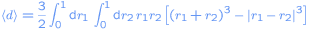This integral can be computed by splitting it into two parts:
.
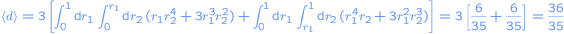Hence, the mean distance between two randomly choosen points within the sphere is 36/35 = 1,02857....
The strange thing of this problem is that it easier to solve in three dimensions than in two! More dimensions almost always implies more problems. Just try to compute the mean distance between two randomly choosen points within a circle.
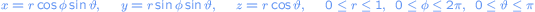
The probability that a randomly choosen point lies in the area of the sphere with sizes
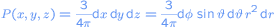
is given byThe distance between two randomly choosen points
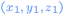and
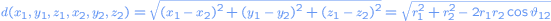
within the sphere iswhere
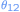is the angle between the points
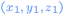and
.
The mean distance between two randomly choosen points within the
sphere is now given by
.
Using spherical coordinates and symmetry, the last formula can be simplified to
.
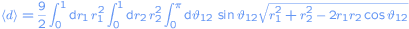Performing the integral over the angle gives
.
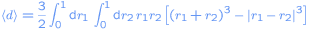This integral can be computed by splitting it into two parts:
.
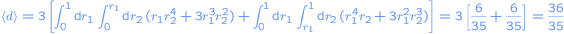Hence, the mean distance between two randomly choosen points within the sphere is 36/35 = 1,02857....
The strange thing of this problem is that it easier to solve in three dimensions than in two! More dimensions almost always implies more problems. Just try to compute the mean distance between two randomly choosen points within a circle.
|
|