Platonic solids - math puzzle
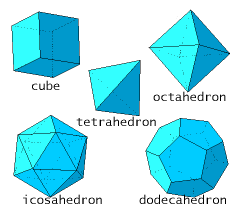
| Show that there exist only five platonic solids (that are objects which are build out of the one sort of regular polygons, like the tetrahedron and the cube). Hint: use that for each solid in three dimensions it holds that the number of vertices + the number of faces is equal to the number of edges + 2. |
|